資産運用をしていく上で、目標金額に対する運用額や運用利率、運用期間の感覚は欠かせません。
しかし、これらは互いに密接に関わっているため、それぞれを自由に捉えることはできません。それを、ビジネスの世界でもよく使われるQCDの関係になぞらえて、これらの関係性をイメージできるようになりましょう。
Contents
QCDとは

まずはじめに、一般的なQCDの話です。
ご存知の方も多いと思いますが、QCDとは元々は製造業における品質とコスト、納期の関係性を示した概念です。
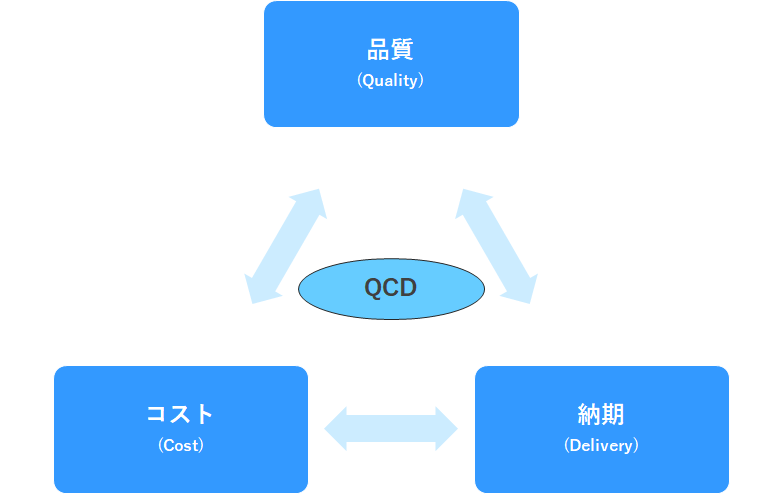
QCDは
- Quality:品質
- Cost:コスト
- Delivery:納期
の頭文字からくるもので、「品質(Q)を高めるためには、コスト(C)をかけ、納期(D)を長く取る必要がある」というようなトレードオフの関係を示すものです。
製品製造においては製品品質が最も大事であるために、頭文字としてもQが真っ先にきていますが、だからといってコストや納期を無視することもできず、「QCD全体のバランスが重要である」ということを示す概念となっています。
QCDそのものについて更に詳しく知りたい方はこのあたりをご覧ください。
お金のQCD

ではこのことを、資産運用にも応用してみましょう。
QCDはトレードオフの関係を示したものですが、それは資産運用でも同じことです。
一般的に、資産運用で大きなリターンを上げるためには大きなリスクを負わなくてはなりませんが、運用期間を長く取ればリスクを少なく済ませることもできます。
そうした観点が相互に影響する様子はまさにQCDと似ているところなので、これをQCDになぞらえて整理してみます。
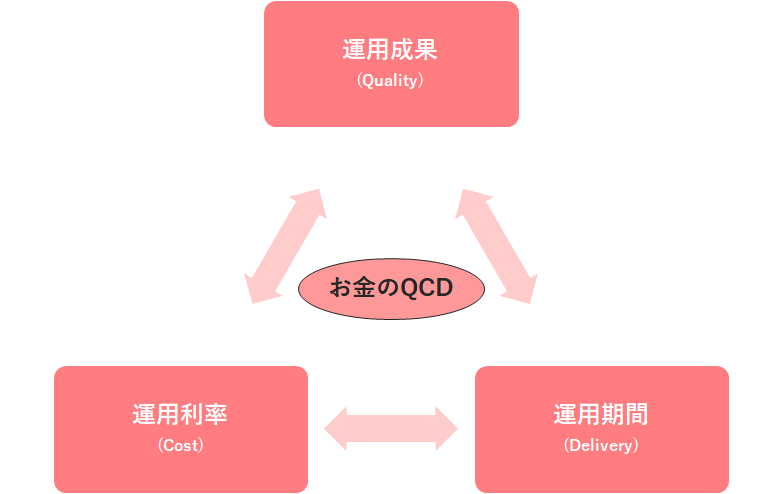
少し強引ですが、このように当てはめてみました。
- Quality:運用成果
- Cost:運用利率
- Delivery:運用期間
先ほども触れた、「高い運用成果を上げるためには、大きな運用利率か長い運用期間が必要」ということをよく表していると思います。
お金のQCDの使い方

それでは実際にお金のQCDを意識するとどんなことが分かるのでしょうか。
いくつかの例を通じて考えてみましょう。
前提
お金のQCDを考える上では、元となる条件を決めておく必要があります。
今回は、
- 運用元金:100万円
- 年積立額:60万円(5万円/月)
だといくつか実際に計算してみましょう。
(あとで自由に計算するフォームも載せておきます)
住宅資金の1,000万円を貯めたい
例えば、自宅購入に向けた頭金として1,000万円が必要になったとしましょう。
月々に捻出できそうな金額はそれなりに決まっていると思いますので、そのペースで1,000万円を貯めようとする場合、どれくらいの運用利率(C)や運用期間(D)が必要になるでしょうか。
運用利率と運用期間を使い、それぞれの運用成果をまとめたのが以下の表です。
| 5年 | 10年 | 15年 | 20年 | 25年 | 30年 | 35年 | |
|---|---|---|---|---|---|---|---|
| 0% | 400万円 | 700万円 | 1,000万円 | 1,300万円 | 1,600万円 | 1,900万円 | 2,200万円 |
| 1% | 413万円 | 742万円 | 1,087万円 | 1,450万円 | 1,832万円 | 2,233万円 | 2,655万円 |
| 3% | 440万円 | 834万円 | 1,291万円 | 1,823万円 | 2,440万円 | 3,157万円 | 3,990万円 |
| 5% | 468万円 | 940万円 | 1,545万円 | 2,321万円 | 3,317万円 | 4,594万円 | 6,233万円 |
| 7% | 499万円 | 1,063万円 | 1,861万円 | 2,992万円 | 4,594万円 | 6,862万円 | 10,073万円 |
| 10% | 549万円 | 1,284万円 | 2,491万円 | 4,470万円 | 7,718万円 | 13,048万円 | 21,794万円 |
こちらはわかりやすい結果ですね。
元金を100万円、年積立額を60万円としているため、15年でちょうど元金が1,000万円になります。
ですので、運用なんかしなくても15年で貯まってしまいますが、運用でそれを早めようと思うとそれなりにリスクを負う必要があるとわかります。
運用率7%で10年1,000万円を超えることができますが、運用率7%を安定して10年間継続するのはなかなか大変ですね。対象としては株のインデックス投資あたりで、好調な期間であればそれも可能ですが、時期が悪いとなかなかそうもいかないことになるでしょう。
運用率5%だと10年で940万円なのでまだ…というところですが、10年間安定して成果を出さないといけないことを考えると、微妙なラインです。
このあたりの結果を踏まえ、自分の考えを整理すると
- 1,000万円貯められないことはないが、10年以上待つのは厳しい
- 見直し例)家計を見直して年積立額を100万円に増額すると、運用率5%でも7年後に1,000万円に到達できそう
- 今の家計ではこれ以上捻出できないが、高すぎるリスクも負いたくない
- 見直し例)目標額を700万円にすると、運用率5%で8年後に700万円に到達できそう
などの見直しに繋げられると思います。
早期リタイアのための5,000万円を貯めたい
さて、次はより実践的に「早期リタイアのため25年以内に5,000万円貯蓄したい」ということを考えてみましょう。
5,000万円という運用成果に加え、25年以内という運用期間の制限も入れたパターンです。
表は先ほどと同じですが、達成水準は以下のようになります。
| 5年 | 10年 | 15年 | 20年 | 25年 | 30年 | 35年 | |
|---|---|---|---|---|---|---|---|
| 0% | 400万円 | 700万円 | 1,000万円 | 1,300万円 | 1,600万円 | 1,900万円 | 2,200万円 |
| 1% | 413万円 | 742万円 | 1,087万円 | 1,450万円 | 1,832万円 | 2,233万円 | 2,655万円 |
| 3% | 440万円 | 834万円 | 1,291万円 | 1,823万円 | 2,440万円 | 3,157万円 | 3,990万円 |
| 5% | 468万円 | 940万円 | 1,545万円 | 2,321万円 | 3,317万円 | 4,594万円 | 6,233万円 |
| 7% | 499万円 | 1,063万円 | 1,861万円 | 2,992万円 | 4,594万円 | 6,862万円 | 10,073万円 |
| 10% | 549万円 | 1,284万円 | 2,491万円 | 4,470万円 | 7,718万円 | 13,048万円 | 21,794万円 |
このようになりました。
まず、「25年以内」という期間制約があるため、30年と35年の選択肢はなくなります。
その残りで改めて5,000万円の運用成果を上げられるのは運用率10%で25年運用するケースだけです。隣接する20年10%か25年7%はまだ近いですが、それでも厳しいところでしょう。
このように、長期的な見通しであっても、実際にシミュレーションしてみると現実離れしたことを言っていることが往々にしてあるので、そうした感覚を直すためにもこうしたお金のQCD感覚が役に立ちます。
リスクを抑えつつ、25年以内に行動したい
最後は少し変わったアプローチですが、「リスクを抑えながら貯蓄をするものの、それによって積み上がる金額を見ながらやることを考えたい」というケースです。
| 5年 | 10年 | 15年 | 20年 | 25年 | 30年 | 35年 | |
|---|---|---|---|---|---|---|---|
| 0% | 400万円 | 700万円 | 1,000万円 | 1,300万円 | 1,600万円 | 1,900万円 | 2,200万円 |
| 1% | 413万円 | 742万円 | 1,087万円 | 1,450万円 | 1,832万円 | 2,233万円 | 2,655万円 |
| 3% | 440万円 | 834万円 | 1,291万円 | 1,823万円 | 2,440万円 | 3,157万円 | 3,990万円 |
| 5% | 468万円 | 940万円 | 1,545万円 | 2,321万円 | 3,317万円 | 4,594万円 | 6,233万円 |
| 7% | 499万円 | 1,063万円 | 1,861万円 | 2,992万円 | 4,594万円 | 6,862万円 | 10,073万円 |
| 10% | 549万円 | 1,284万円 | 2,491万円 | 4,470万円 | 7,718万円 | 13,048万円 | 21,794万円 |
「リスクを抑える≒運用利率3%以内」とした場合の考えですが、このような結果となります。
25年で最大2,500万円程度は見えますが、例えば20年3%の1,800万円で行動をはじめるという捉え方もできるでしょう。
先ほどまでは高望みした自分を自制していくパターンでしたが、こちらは高望みをせず現実に自分を合わせていくような考え方です。
お金のQCDを計算してみよう
お金のQCDがそれぞれ関係していることはここまでのことでわかったと思いますが、実際にどういう関係なのかはまだしっくりきていないと思います。
というわけで、以下にシミュレーションフォームを用意したので、各設定で結果がどのように変わるか試してみてください。
お金のQCDシミュレーションフォーム
運用元金、年積立額、運用利率、運用期間の数字をもとに、複利運用によっていくらの運用成果が出るかを計算するフォームです。
計算式の詳細
上のフォームが具体的にどういう計算式になっているのか一応書いておきます。
自分用にExcelなんかで関数を組みたい人は参考にしてみてください。
$$ \begin{eqnarray} \left\{ \begin{array}{l} M := 運用元金(万円) \\ m := 年積立額(万円) \\ \\ q := 運用成果(万円) \\ c := 運用利率(\%) \\ d := 運用期間(年) \\ \\ q = M \times (1+c)^d + m \times \cfrac{(1+c)^d-1}{c} \\ \end{array} \right. \end{eqnarray} $$参考: 72の法則
べき乗が入るためになかなか暗算できない複利計算ですが、簡単な近似計算の方法として、次の72の法則が知られています。
72の法則
年利 c %で複利運用したとき、元本が2倍になるまでの年数は、おおよそ72を年利 c で割った値に等しい。
文章で見るとよくわかりませんが、要するにこういうことです。
$$ \begin{eqnarray} \left\{ \begin{array}{l} c := 運用利率(\%) \\ d := 元本が2倍となる運用期間(年) \\ \\ d \approx \cfrac{72}{c} \end{array} \right. \end{eqnarray} $$実際に、72の法則による値と厳密な計算による値を比べると以下のように確かに近しい値になっていることがわかります。
| 72の法則 | 正確な値 | 誤差 | |
|---|---|---|---|
| 1% | 72.0年 | 69.7年 | 3.36% |
| 2% | 36.0年 | 35.0年 | 2.85% |
| 3% | 24.0年 | 23.4年 | 2.35% |
| 4% | 18.0年 | 17.7年 | 1.85% |
| 5% | 14.4年 | 14.2年 | 1.36% |
| 6% | 12.0年 | 11.9年 | 0.88% |
| 7% | 10.3年 | 10.2年 | 0.40% |
| 8% | 9.0年 | 9.0年 | -0.07% |
| 9% | 8.0年 | 8.0年 | -0.54% |
| 10% | 7.2年 | 7.3年 | -1.00% |
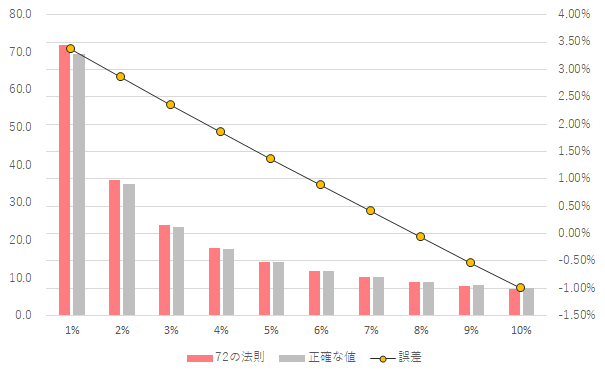
概ね正確ですが、あくまで近似計算なので「8%のところでもっともよい近似になっている」ことは覚えておいたほうがよいでしょう。
とはいえ、2%より上のところでは誤差が1年未満になっていくため、感覚を掴むくらいであれば十分実用的だと思います。
ちなみに、原理的には72の法則ではなく、69の法則になることがよりよい近似になるのですが、「1-10%付近での近似度が高くなるようにする」「より多くの約数があり、使い勝手の良い数字を選ぶ」観点から意図的に72に補正されているようです。
近似度だけであれば69~73くらいが妥当ですが、確かにこの中で最も使い勝手がいい数字といえば72で納得ですね。詳しくはこちらの記事でどうぞ。
まとめ
資産運用の勉強をしていくと、複利の力を知り、長期間継続的に投資していくことで今の感覚よりはるかに大きな資産を作ることができると分かります。
しかし、だからといってその力を過信しすぎるのも禁物で、計画の妥当性を評価する上でも、まともな感覚を持っておく必要があります。
これは詐欺に対する防御策としても有効で、「5年後には倍になる」と言われたときに、このQCD感覚をもって「年利30%近い計算になるのでさすがにおかしい」などと判断することができます。
厳密な計算はもちろんパソコンなりの機会に頼らざるを得ないものの、大雑把な感覚だけでもこうして知っておくと役立つ場面が多いのではないでしょうか。
参考記事
今回紹介したようなお金のQCD感覚を、より一般的に金融リテラシーとする場合、金融庁などが作成した金融リテラシー・マップが役に立ちます。